Basic Formulas Of Algebra P2

            

       Basic Of Algebra

Hi Friends!!

Let's discuss about the Algebra.....

                                                                      

Algebra: In Mathematics another part is there called Algebra here you can read about constants, Variables, and arithmetic operations.

example:     With two variables (x, y)

                        2x+3y=5,  3x+7y=10.

                        here    2,3,5,3,7,10 are Constant.

                        x and y   are two Variable.

                        +,=   are Arithmetic Operations.

                                                 example:     With one variables(x or  y)

                                                                      In x Variable

                                                                      2x+3=5.  

                                                                

                                                                        or

                                                                     In y Variable

                                                                   

                                                                     2y+3=5.

Both equations are same only Variable name is Different, finally output will be same.

                                                                            

Brief History: The word "Algebra" is derived from the Arabic word الجبر al-jabr, and this comes from the treatise written in the year 830 by the medieval Persian mathematician, Muhammad ibn Mūsā al-Khwārizmī.

If you want to read about Algebra then must know about some Basic Formula.

I am describing the important formulas.

First try to read the each terms then below I will mention all Formulae so that you can read the All formulae with better Understand. 

Now all formulas :

Note:  No need to remember, just practice questions based on the Formulae that I mentioned but keep in mind do practice with Honesty.

Important Formulas in Algebra.

now....

Having power 2

• a2 – b2 = (a – b)(a + b)
• (a + b)2 = a2 + 2ab + b2
• a2 + b2 = (a + b)2 – 2ab
• (a – b)2 = a2 – 2ab + b2
• (a + b + c)2 = a2 + b2 + c2 + 2ab + 2bc + 2ca
• (a – b – c)2 = a2 + b2 + c2 – 2ab + 2bc – 2ca
• (a + b + c + …)2 = a2 + b2 + c2 + … + 2(ab + ac + bc + ….)

Having power  3

• (a + b)3 = a3 + 3a2b + 3ab2 + b3 ; (a + b)3 = a3 + b3 + 3ab(a + b)
• (a – b)3 = a3 – 3a2b + 3ab2 – b3 = a3 – b3 – 3ab(a – b)
• a3 – b3 = (a – b)(a2 + ab + b2)
• a3 + b3 = (a + b)(a2 – ab + b2)

Having power 4

• (a + b)4 = a4 + 4a3b + 6a2b2 + 4ab3 + b4
• (a – b)4 = a4 – 4a3b + 6a2b2 – 4ab3 + b4
• a4 – b4 = (a – b)(a + b)(a2 + b2)

Having power  5

• a5 – b5 = (a – b)(a4 + a3b + a2b2 + ab3 + b4)

Having power n

• If n is a natural number an – bn = (a – b)(an-1 + an-2b+…+ bn-2a + bn-1)

• If n is even (n = 2k), an + bn = (a + b)(an-1 – an-2b +…+ bn-2a – bn-1)
• If n is odd (n = 2k + 1), an + bn = (a + b)(an-1 – an-2b +an-3b2…- bn-2a + bn-1)

• Laws of Exponents (am)(an) = am+n ; (ab)m = ambm ; (am)n = amn 

           Here m, n  is any RealNumber.

• Fractional Exponents a0 = 1 

          Here a  is any RealNumber.

For Quadratic Equations

• Roots of Quadratic Equation

• For a quadratic equation  ax2 + bx + c = 0  where  a ≠ 0,  the roots will be given by the equation as  

                 x lower  +  means Adding values, and similar for x negative.

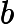
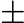
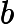
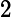
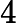
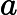
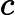
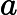
• Δ = b2 − 4ac  is called the discriminant

• For real and distinct roots, Δ > 0

• For real and coincident roots, Δ = 0

• For non-real roots, Δ < 0

• If α and β are the two roots of the equation  ax2 + bx + c = 0  then,  α + β = (-b / a)  and  
• α × β = (c / a).

• If the roots of a quadratic equation are  α   and    β,  the equation will be  (x − α)(x − β) = 0.

Graphical Analysis of Quadratic Equation:

  first let's take a basic Quadratic Eq.

  y = x²

The Graph of the equation is...

Parabola.

Look it is passing though (0,0) means x=0 and y=0.

This graph can be drawn by putting different value of 'x'. Since you know corresponding to 'x' we  get a 'y' value also then draw axis and mark the point then join the points properly.      

                                                           

                 By Using the same concept you can Analyze  the Quadratic Equation :

  y=ax2 + bx + c  

here a ≠ 0,

Case 1: if a>0  i.e Positive,  then Graph of the above equation is..

Opening up Parabola since a>0.

Case 2: if a<0  i.e Negative,  then Graph of the above equation is..

Closing Down Parabola since a<0.

Now, In General form

Let's Take an Example :

     Draw the Graph of the below Equation:

y=x2+2x+1$$$$

Make a table of value for some values of x. Use both positive and negative values!

x	y = x2 + 2x + 1
-3	4
-2	1
-1	0
0	1
1	4
2	9
3	16

Graph the points and draw a smooth line through the points and extend it in both directions

Vertex:  x=−b2a=−22⋅1=−1

Hence the coordinate of Vertex is (-1,0).

So by using these concept you can how to draw the graph of any Quadratic Equations.

   Note:  you have already read , how to find roots of Quadratic Equations by using 

   Standard formula.

Finding the number of Roots  of Quadratic  Equation's by looking their Graphs.

        Note:  If you want to find the No. of roots o0f Quadratic Equations by Graph method just                remember the basic Points.

• Always find number of Intersecting point on the X-Axis Only.

        So here three case possible:

1. The Graph may intersect the X-Axis.
2. The Graph may not intersect the X-Axis
3. The Graph may Touch the X-Axis only.          

   

Look in Graph Two Real Roots, here X-Axis is being intersected at two points, so it has Two Roots, Since Intersecting at Real Axis so these roots are Real roots.

Look in Graph One Real Root, here X-Axis is being intersected at one point, so it has One Root, Since Intersecting at Real Axis so this root is Real root.

Note: All Quadratic Equation has at least two roots. here saying   One Real Root means Both roots are Equal so saying One Real Root.

Look in Graph Imaginary Roots ,here X-Axis is not being intersected at Any point, so it has No real Root, Since Intersecting point is Not at X-Axis so Both Roots are Imaginary.

Observed Point:

In a Graph you can find the no of roots as well Nature of Roots, just by looking Intersecting Points at X-axis.

Let's take an Example of general Graph.  

 

Note:  If  a Graph intersects at Negative side of X-Axis then roots will Negative  and if it intersects at Right side of X-Axis then roots will Positive.

And if it is Passing though Origin (0,0) then Root is Zero (0).

Note:  The above Graph has Maximum  4  real roots.

Number of roots of any Graph = Maximum Power in Polynomial.

Conclusion:  Now you can find the number of roots and Nature of Roots of Any graph by just looking the Graph. But that graph must intersect the X-Axis, if not intersects then Look the Polynomial of specific Graph then you can easily find out Number of 

Roots as well Nature of Roots (Real Roots  or Imaginary Roots).

Thanks!

Happy Learning :)

he