About Two variables Equations P5

By ·


         About Two Variables Equations


Let's talk about Two Variables Equations...


Constant: In Mathematics whose value does not change at any cost, called Constant.

Example: Pi (stylized as π),  Coefficient of Quadratic Equations.

               3x+6y=0.

               here 3 and 6  are constant. 





Variable: In Mathematics whose value changes, called Variable.

Example: x + y=2.  

here x and y are Variable since we can put here any value to achieve result as 2.

Possibilities
x=1 , y=1.

x=0.5, y=1.5.

x=.2, y=1.8.

....   so we can see here values Changes of the Variable x, y.




Single Variable: If any mathematical expression has only one variable then it is called Single Variable.

Example:  2x+7=0.   9y+7=8.

Here, look in two equations,  each has only one Variable either x or y.




Two Variable: If any mathematical expression has Two variables then it is called Two Variable.

Example:  2x+7y=0.   9x+7y=8.

Here, look in two equations,  each has  Two Variables x and y.





Multi Variable: If any mathematical expression more than Two variables then it is called Multi Variable.

Example:  2x+7y+5z=0.   9x+7y+4z+8u=8.

Here, look in two equations,  each has more than Two Variables.




RHS and  LHS in Equation: Let's assume the Equation, give below

        2x+4y                          =             4x+9
 
LHS(Left Hand Side)             RHS(Right Hand Side).  corresponding.




Two lines Possibilities:

If you have Two Straight Line then how many possibility so that they can make a relation with each other (Think....)


Let's see by taking scenario,

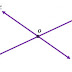
Case1:  If Two Straight Line intersect at an angle, called Intersecting Line.



Here Two Straight Line AB and CD intersect at point O (ओ) in a Plane.



Suppose you have given some Equations and saying check whether the given equations represent these Lines or not?


So I am  going to tell you it is very simple............

Let's say x, y Two Variables,
  a1, b1, c1, a2, b2, c2 are Real Number where  a1^2+b1^2 ≠ 0, and  a2^2+b2^2 ≠ 0,

then Equations,

,  

 a1 / a2 ≠ b1 / b2.

Then Line will Intersect to Each other.


Example: x-2y=0 and 3x+4y-20=0

Here from the Equation,

a1/a2= 1/3,

b1/b2=  -2/4,

c1/c2=  0/-20.

so,

1/3 ≠ -2/4

Look Condition from above, is it satisfying.....?

 a1 / a2 ≠ b1 / b2.

of course Yes,  this condition is satisfying, so Above Equation of Line will Intersect to each other.


Note: By using same concept you can find whether the Equation of Line will Intersect or not.



Remark: The above  pair of linear equations is consistent. This means there is unique solution for the given pair of linear equations. The graph of the linear equations would be two intersecting lines.


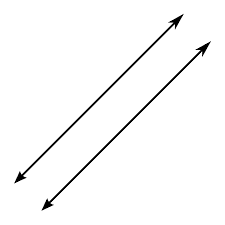
Case2: If Two Straight Line Parallel to each other.



Here Both Line are Parallel in plane.


Suppose you have given some Equations and saying check whether the given equations represent the above Lines or not?


So I am  going to tell you it is very simple............

Let's say x, y Two Variables,
  a1, b1, c1, a2, b2, c2 are Real Number where  a1^2+b1^2 ≠ 0, and  a2^2+b2^2 ≠ 0,

then Equations,

,  

 a1 / a2=b1 / b2 ≠c1 / c2 .

Then Line will Parallel to Each other.


Example: x+2y-4=0 and 2x+4y-12=0

Here from the Equation,

a1/a2= 1/2,

b1/b2=  2/4,

c1/c2=  -4/-12.

so,

1/2 =  2/4  ≠ - 4/-12



Look Condition from above, is it satisfying.....?

 a1 / a2 = b1 / b2  ≠ c1 / c2 

of course Yes,  this condition is satisfying, so Above Equation of Line will Parallel to each other.


Note: By using same concept you can find whether the Equation of Line will Parallel or not.


Remark: The pair of linear equations is inconsistent. This means there is no solution for the given pair of linear equations. The graph of linear equations will be two parallel lines.


Case3: The lines which coincide or lie on top of each other are called coincident lines.




Here one Line is lying on top of other and may be in any directions.



Suppose you have given some Equations and saying check whether the given equations represent the above Lines or not?


So I am  going to tell you it is very simple............

Let's say x, y Two Variables,
  a1, b1, c1, a2, b2, c2 are Real Number where  a1^2+b1^2 ≠ 0, and  a2^2+b2^2 ≠ 0,

then Equations,

,  

 a1 / a2 = b1 / b2 = c1 / c2 .

Then Line will Coincident to Each other.


Example: 2x+3y-9=0 and 4x+6y-18=0

Here from the Equation,

a1/a2= 2/4,

b1/b2=  3/6,

c1/c2=  -9/-18.

so,

2/4 =  3/6  = - 9/-18



Look Condition from above, is it satisfying.....?

 a1 / a2 = b1 / b2  = c1 / c2 

of course Yes,  this condition is satisfying, so Above Equation of Line will Coincident   to each other.


Note: By using same concept you can find whether the Equation of Line will Coincident or not.


                

 Remark: The pair of linear equations is dependent and consistent. This means there are infinitely many solutions for the given pair of linear equations. The graph of linear equations will be coincident lines.






Thanks!

Happy Learning :)
                    
                                        










                                 

2 comments: